排序算法的介绍

排序也称排序算法(Sort Algorithm)，排序是将一组数据，依指定的顺序进行排列的过程。

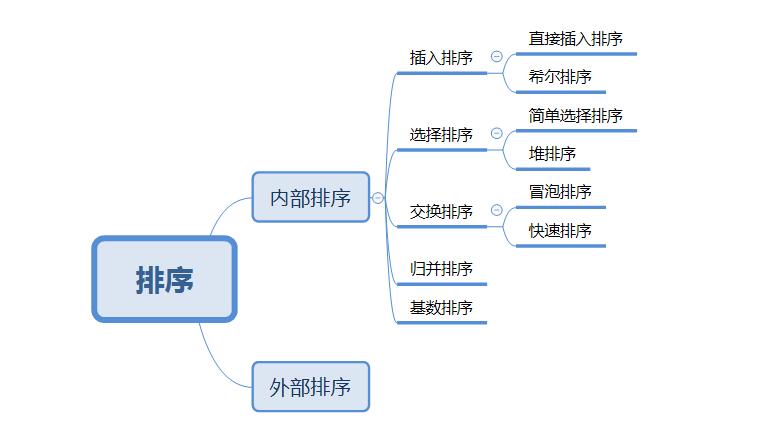
排序的分类

​ 1.内部排序：

​ 指将需要处理的所有数据都加载到内部存储器（内存）中进行排序。

​ 2.外部排序：

​ 数据量过大，无法全部加载到内存中，需要借助外部存储（文件等）进行排序。

​ 3.常见的内部排序算法：

​

冒泡排序

冒泡排序（Bubble Sorting）的基本思想是：通过待排序序列从前向后（从下标较小的元素开始），依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就像水滴的气泡逐渐向上冒。

一句话概括：先找大的，找到了就按先后顺序往末尾移动。

思路很简单，就是把在前面通过比较相邻的两个数，遍历数组找到最大的，移动到数组的末尾

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int[] bubbleSort(int[] array){
    int temp = 0;
    boolean flag = false;
    for (int i = 0; i < array.length - 1 ; i++) {
        for (int j = 0; j < array.length -1 -i  ; j++) {
            if (array[j] > array[j+1]){
                 temp = array[j];
                 array[j] = array[j+1];
                 array[j+1] = temp;
            
            }
        }
    }
    return array;
}

可以在图示中看到，在第三趟排序退出时，数组已经是有序的了，但还是依然会走第四趟排序，再与相邻元素进行比较，所以可以优化，加入标志位，判断是否进入交换 if (array[j] > array[j+1])中，未进入，说明数组已经是有序的了，直接返回即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static int[] bubbleSort(int[] array){
    int temp = 0;
    boolean flag = false;
    for (int i = 0; i < array.length - 1 ; i++) {
        for (int j = 0; j < array.length -1 -i  ; j++) {
            if (array[j] > array[j+1]){
                 temp = array[j];
                 array[j] = array[j+1];
                 array[j+1] = temp;
                flag = true;
            }
        }
        if (!flag) {
            break;
        }else {
            flag = false;
        }
    }
    return array;
}

选择排序

一句话来说：把最小的值提到数组前面，在数组的首部逐步有序化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void selectSort(int[] array){
        //假定第一个是最小
        int minIndex = 0;
        int min = array[0];
        for (int j = 0; j < array.length - 1; j++) { 
          //交换次数 n- 1  与冒泡一样 时间复杂度O(n^2)
          //假定最小的值，其索引为0，遍历数组，找到真正最小的值，交换，然后将0索引后移一位，找到第二小的
             minIndex = j;
             min = array[j];
            for (int i = minIndex +1; i < array.length; i++) {
                if (array[i] < min){
                    minIndex = i;
                    min = array[i];
                }
            }
            //将找到的最小值与假定的最小值进行交换-- 交换排序的核心
            array[minIndex] = array[j];
            array[j] = min;
            System.out.println(Arrays.toString(array));
        }
        System.out.println("最终-"+Arrays.toString(array));

    }
}

对比冒泡排序和选择排序，前者找最大的放末尾，后置找最小的放首部，感觉这完全就是一种算法吧，在冒泡在改变条件，也可以实现这样的效果，其实并不这样，这两种算法虽然表面是兄弟，但实现思想却不一样：

冒泡是在从索引为0的元素相邻之间逐个比较，最后把最大元素放到最后，没错是相邻之间，一直进行比较和交换。

选择排序又是基于另一种算法思想，假定索引为0的元素是最小，遍历数组，看有不有更小的，直到遍历完全，保存最小元素的索引，最后进行交换，而不是每次一比较就交换。

插入排序

插入排序就是把数组分成有序和无序的两部分，每次取到无序部分的元素，把它放在有序部分的合适位置，实现数组的逐步有序化。

R[0] R[1] R[2] R[3] R[4] R[5]
初始状态 （17） 3 25 14 20 9
第一次插入 （3 17） 25 14 20 9
第二次插入 （3 17 25） 14 20 9
第三次插入 （3 14 17 25） 20 9
第四次插入 （3 14 17 20 25） 9
第五次插入 （3 9 14 17 20 25） 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
 public static int[] insertSort(int[] array){

        //待插入的数
        int insertVal = array[1];
        int insertIndex = 1 -1; //即arr[1] 的前面这个数的下标

        for (int i = 1; i < array.length ; i++) {
            insertVal = array[i];
            insertIndex = i -1; //即arr[1] 的前面这个数的下标

            //insertIndex >=0 不越界
            //insertVal < array[insertIndex] 说明insertVal比有序数组中的任意数都要小（因为array[insertIndex]就是最大的）
            //现在需要找到insertVal合适的位置即可
            //若不满足，拿insertVal比有序数组最大的都大  直接放在有序数组的最后面
            while (insertIndex >=0 && insertVal < array[insertIndex]){ //插入到有序数组中
                array[insertIndex + 1] = array[insertIndex];
                insertIndex -- ; //找到待插入数合适的位置
            }
            array[insertIndex + 1] = insertVal;
          //  System.out.println("第"+i+"轮："+ Arrays.toString(array));
        }
        return array;

    }
}

希尔排序

希尔排序是针对普通插入排序排序存在的问题而提出的，假如数组中较小的元素在数组的末尾，在找最后一个元素合适位置的时候，while循环次数很多，效率不高，希尔排序通过设置增量实现效率的极大提升！

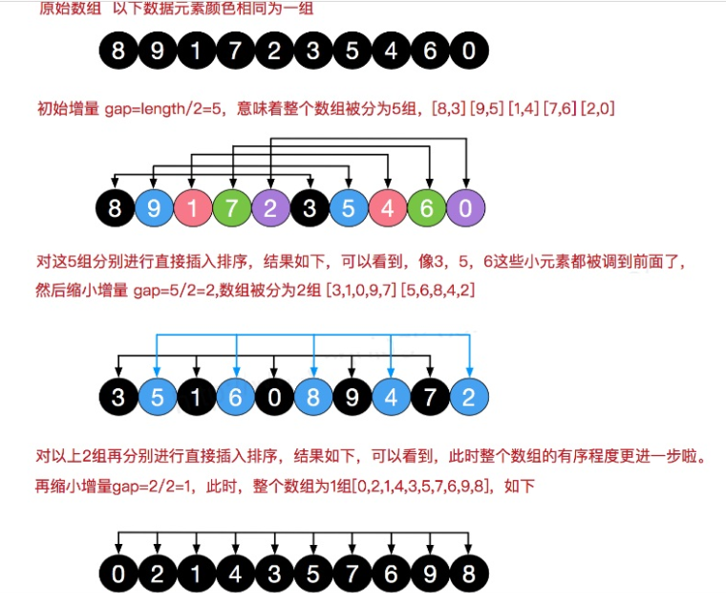
可以看到，思想确实很好，类似一个宏观调控，对数组简单的微调，无需大量移动操作即可完成整个数组的排序。

但通常有两种实现方式，一种是交换法，在每次分组后，元素就要完成交换，小的在前，大的在后；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * 交换法
 * @param array
 */
public static void shellSort(int[] array){
    int length = array.length;
    int temp = 0;
    for (int n = length / 2; n >=1; n/=2) {
        for (int i = n; i < length; i++) {
            for (int j = i -n; j >= 0; j-=n){
                    if (array[j] > array[j+n]){
                        temp = array[j+n];
                        array[j+n] = array[j];
                        array[j] = temp;
                    }
            }
        }
    }
}

这也是最好理解的，但效率低于用移位法实现的希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
  /**
     * 移位法
     * @param array
     */
    public static void shellSort2(int[] array){
        for (int gap = array.length / 2 ; gap >=1 ; gap /= 2){
            for (int i = gap; i < array.length; i++) {
                int j =i;
                int temp = array[j];
                if (array[j] < array[j - gap]){
                    while (j - gap >=0 && temp < array[j - gap]){
                        array[j] = array[j -gap];
                        j -= gap;
                    }
                    array[j] = temp;
                }
            }
        }
    }
}

可以看到，移位法类似插入排序，都是while循环找到元素最终的位置，再进行移动，减少元素交换所消耗的时间。

快速排序

快速排序(Quicksort)是对冒泡排序的一种改进。

基本思想是:通过一趟排序将 要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

一句话概括：分组排序！

提到分组，可能很多朋友看到这会想到分治算法了吗？这里的我说是分组就是递归的意思，后面的归并排序才是分治算法的一个实践。

快排有很多实现方法，主要的区别就是选取的标准不一样，有点找末尾，有点选中间，但操作都是大同小异，通过标准数第一次把数组分成左右两部分，然后对左右两部分分别进行递归，递归结束，数组也就变得有序了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
    public static void quickSort(int[] array,int left,int right){
        int l = left;
        int r = right;
        int temp = 0;
        //pivot 中轴
        int pivot = array[(left + right) / 2];

        while (l < r){
            while (array[l] < pivot){
                ++l;
            }
            while (array[r] > pivot){
                --r;
            }
            if (l >= r){
                break;
            }

            temp = array[l];
            array[l] = array[r];
            array[r] = temp;

            if (array[1] == pivot){
                --r;
            }
            if (array[r] == pivot){
                ++l;
            }
        }

        //防止l = r 很重要！
        if (l == r){
            ++l;
            --r;
        }
        //向左递归
        if (left < r){
            quickSort(array,left,r);
        }
        //向右递归
        if (right > l){
            quickSort(array,l,right);
        }
        //System.out.println(Arrays.toString(array));
    }
}

这里我们测试下五种排序算法的效率

随机生成10W条数据的数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class Test {
    public static void main(String[] args) {
        int[] array = new int[100000];
        for (int i = 0; i < 100000; i++) {
            array[i] = (int) (Math.random()*100000);
        }
//        int[] array = {2,5,3,6,9,4,500,200,40};
        long start = System.currentTimeMillis();

//        bubble(array);  //所花费时间17411ms
//        select(array); //所花费时间3229ms
//        insert(array); //所花费时间1003ms
//        shell(array);  //所花费时间18ms
        quick(array);  //所花费时间22ms
        long end = System.currentTimeMillis();
        System.out.println("所花费时间"+(end - start) +"ms");
    }

    public static void bubble(int[] array){
        BubbleSort.bubbleSort(array);
    }
    public static void select(int[] array){
        SelectSort.selectSort(array);
    }
    public static void insert(int[] array){
        InsertSort.insertSort(array);
    }
    public static void shell(int[] array){
        ShellSort.shellSort2(array);
    }
    public static void quick(int[] array){
        QuickSort.quickSort(array,0,array.length -1);
    }
}

希尔排序和快排效率确实较前三种排序算法要高很多，后面的三种排序放下一篇讲!